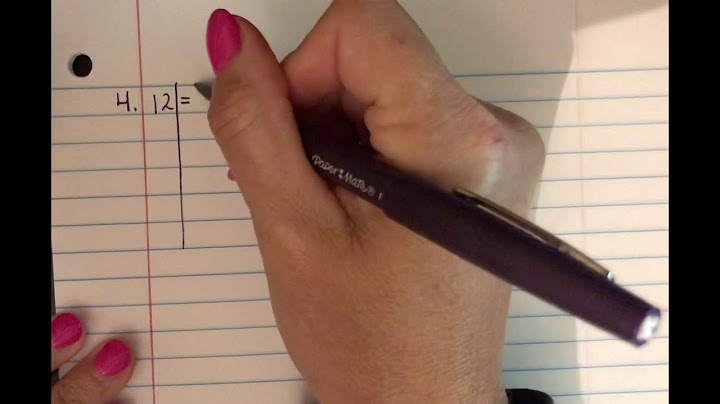Solving system of differential equations with initial conditions

Coupled Systems

What is a coupled system?

A coupled system is formed of two differential equations with two dependent variables and an independent variable.

An example -

where a, b, c and d are given constants, and both y and x are functions of t.

How do we solve coupled linear ordinary differential equations?

Use elimination to convert the system to a single second order differential equation. Another initial condition is worked out, since we need 2 initial conditions to solve a second order problem. Solve this equation and find the solution for one of the dependent variables (i.e. y or x). Use this solution to work out the other dependent variable.

For example:

How do we solve

 
   (1)

 
   (2)

with initial conditions

and

?

Step 1: First make x the subject of (1),

.

Step 2: Substitute in (2) to get

which simplifies to

with initial conditions

and

.

Step 3: The roots of the auxiliary equation

are 2, 1. Hence the solution to the homogeneous problem is

.

Step 4: Substituting the initial conditions gives

i.e.

.

Step 5: Now we have

. Hence the solution is

and

.

Test Yourself

Our online expert tutors can answer this problem

Get step-by-step solutions from expert tutors as fast as 15-30 minutes. Your first 5 questions are on us!

Number Line

How do you solve a system of differential equations?